Directed algebraic topology

In mathematics, directed algebraic topology is a form of algebraic topology that studies topological spaces equipped with a direction. The generic term directed spaces is applied to such spaces. Directed algebraic topology is a subject that emerged in the 1990s to meet the need for models of Concurrency (computer science). Its domain is distinguished from classical algebraic topology by the principle that directed spaces have privileged directions and that the directed paths therein need not be reversible. Its homotopical tools, corresponding to ordinary homotopies, fundamental groups and fundamental n-groupoids, are similarly 'non-reversible': directed homotopies, fundamental monoids and fundamental n-categories. Its applications deal with domains where privileged directions appear, like concurrent processes, traffic networks, spacetime models, noncommutative geometry, rewriting systems and the modelling of biological systems.^[1]

1 Directed Spaces
2 Directed Homotopies between Directed Paths
3 The Fundamental Category
- 3.1 Some properties
4 The Category of Components
5 Topics
6 References
7 Further reading

Directed Spaces

Many mathematical definitions have been proposed to formalise the notion of directed space. Historically E. W. Dijkstra introduced a simple dialect to deal with semaphore (programming), the so-called 'PV language', and provide each PV program an abstract model: its 'geometric semantics'. Any such model admits a natural partially ordered space (or pospace) structure i.e. a topology and a partial order^[2]. The points of the model should be thought of as the states of the program while the partial order is the 'causality' relation between states. Following this approach, the directed paths over the model i.e. the monotonic continuous paths, represent the execution traces of the program. Yet, from computer science point of view, the pospaces have a severe drawback. Indeed, due to the antisymmetry of partial orders, their only directed loops i.e. directed path which end where they start, are the constant ones. Inspired by smooth manifold, L. Fajstrup, E. Goubault, and M. Raussen use the sheaf (mathematics) theoretic approach to define the local pospaces^[3]. Roughly speaking, a local pospace is a topological space together with an open covering whose elements come with a partial order. Of course, given two elements U and V of the covering, it is required the partial orders on U and V matches on the intersection. Though local pospaces allow directed loops, they form a category whose colimits – when they exist – may be rather ill-behaved. Remarking the directed paths of a (local) pospace appear as a by-product of the (local) partial order – though they contain most relevant information about direction – Marco Grandis define the d-spaces^[4] as topological spaces endowed with a collection of paths – whose members are said to be directed – such that any constant path is directed, the concatenation of two directed paths is still directed, and any subpath of a directed path is directed. The d-spaces allow non constant directed loops and form a category enjoying properties similar to the ones enjoyed by the category of topological spaces. As shown by Sanjeevi Krishnan, the drawbacks of local pospaces can actually be avoided if we extend the notion of pospaces by mean of 'cosheaf'. The notion of stream^[5] is defined this way. More precisely one considers preorders on open subsets and one requires that given any open subset U and any open covering Ω of U, the preorder associated with U is 'generated' by the preorders associated with each member of Ω. The resulting category behaves as nicely as the category of d-spaces. Indeed both of them one can define the directed geometric realization of cubical set (simplicial set) so that its underlying topological space is the (usual) geometric realisation. Actually there is a natural embedding G of the category of streams into the category of d-spaces. This embedding admits a left adjoint functor F. In fact the images of F and G are isomorphic, an isomorphism being obtained by restricting F and G. In some sense, the category of d-spaces can be seen as one of most general formalisation of the intuitive notion of directed space.

Directed Homotopies between Directed Paths

Regardless of the kind of directed space on considers (pospaces, local pospaces, d-spaces or streams) there is an obvious forgetful functor to the category of topological spaces. Given two directed paths γ and δ, a directed homotopy from γ to δ is a morphism of directed spaces h whose underlying map U(h) is a homotopy –in the usual sense– between the underlying path (topology) U(γ) and U(δ). In algebraic topology, there is a homotopy from α to β if and only if there is a homotopy from β to α. Due to non-reversibility, this is no longer true for directed homotopies. As a consequence, we define the congruence 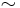$\sim$ as the least equivalence relation on the directed paths which is compatible with concatenation and relates γ to δ as soon as there is a directed homotopy from γ to δ. Going back to the computer science motivation where directed paths represent execution traces, directed homotopies provide a way to identify execution traces. Hence, given a directed space X which models some concurrent program P, the topology of X can be seen as the 'local commutations' of actions in the program P. In classical models of concurrency like 'asynchronous graphs' of 'Mazurkiewicz traces', the local commutations are provided by a relation over the arrows or the actions.

The Fundamental Category

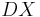The fundamental category of a directed space is defined by mimicking the construction of the fundamental groupoid^[6]^[7] of a topological space. More precisely given a directed space $X$ , we consider the (small) category $DX$ of directed paths over $X$ up to monotonic reparametrisation^[8] and define the fundamental category of $X$ as the quotient $\pi_1(X)\�:=\ DX/\sim$ . 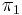This construction gives rise to a functor $\pi_1$ from the category of directed space to the category of small categories.

Some properties

The fundamental category functor satisfies some kind of Seifert–van Kampen theorem.

The fundamental category functor preserves binary products.

As a consequence of the antisymmetry, the fundamental category C of a pospace is loop-free i.e. for all objects x and y, if both homsets C(x,y) and C(y,x) are nonempty, then x=y and C(x,x) is a singleton.

Two directed paths γ and δ sharing the same image i.e. {γ(t) | t∊dom(γ)} = {δ(t) | t∊dom(δ)} are dihomotopic i.e. γ ~ δ. This property obviously fails in algebraic topology e.g. consider paths winding around the circle.

Given X the model of some concurrent program P, the homsets of the fundamental category of X are countable. In addition, if no looping instruction occurs in P, then the homsets of X are finite. This is the case when P is a PV program in the sense originally given by Dijkstra. In comparison all the non trivial homsets of the category of directed paths DX are uncountable.

The Category of Components

While the Fundamental Category construction drastically reduces the size of the homsets of DX, it leaves its collection of objects unchanged. And yet, if X is the geometric model of some concurrent program P, this collection is uncountable. The Category of Components was introduced to find a full subcategory of the Fundamental category with as few objects as possible though it contains all the relevant information from the original^[9]. 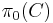If $C$ is a loop-free category, then its category of components $\pi_0(C)$ can be described in the language of Category Theory without assuming $C$ is the fundamental category of some directed space. 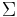In this case the intuitive notion of insignificant morphisms is formalised as a collection $\Sigma$ of morphisms of $C$ satisfying some stability properties and whose elements both preserve the past of their source and the future of their target. 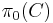Then $\pi_0(C)$ is defined as the quotient^[10] 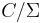$C/\Sigma$ which is proven to be equivalent to the localization of a category $C[\Sigma^{-1}]$ ^[11]. 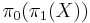The category of components of a PV program P is then defined as $\pi_0(\pi_1(X))$ where $X$ is the geometric model of P. As an interesting property, the category of components of any PV program is finite.

Topics

Higher Order Directed Homotopy

The higher order directed homotopy theory can be developed through cylinder functor and path functor, all constructions and properties being expressed in the setting of categorical algebra $^{[1]}$ . This approach emphasizes the combinatorial role of cubical sets in directed algebraic topology.

The Model Catogory approach

Philippe Gaucher proposed an alternative formalisation of the notion of directed space which is, roughly speaking, based on directed graph enriched in topological spaces i.e. the collection of arrows from x to y is endowed with a topology. This approach gives rise to the so-called category of Flows. This category admits a nontrivial model category structure.

Thomas Kahl proved the existence of a nontrivial model category of pospaces. Yet this structure barely differs from the model structure over topological spaces. To many regards it just consists of forgetting the partial order of the objects.

Krzysztof Worytkiewicz uses advanced methods from model category theory (namely localization and completion) to build a model category from the small categories of finite dimensional directed hypercubes.

In fact any attempt to define a model structure over some category of directed spaces has to face the following question: should an inclusion map $\{*\}\hookrightarrow[0,1]$ be a cofibration, a weak equivalence, both (trivial cofibration) or none. For example, if we suppose $\{0\}\hookrightarrow[0,1]$ is a trivial cofibration, then $\{0\}\times[0,1]\cup[0,1]\times\{0\}$ (as a subpospace of the directed plane) is equivalent to a point since the collection of trivial cofibrations is stable under pushout^[12] . This fact is prohibitive for computer science application though it is a trivial fact from homotopy theory if we drop the direction feature.

Directed Coverings

...

Software

...

References

^ Directed Algebraic Topology: Models of Non-Reversible Worlds, Marco Grandis, Cambridge University Press, ISBN 9780521760362
^ Topology and Order. Leopoldo Nachbin, Van Nostrand Company, 1965
^ Algebraic Topology and Concurrency L. Fajstrup, E. Goubault, and M. Raussen, Theoretical Computer Science, 357, 2006, 241-278
^ Directed homotopy theory, I. The fundamental category Marco Grandis, Cahiers Top. Géom. Diff. Catég 44 (2003), 281-316
^ A Convenient Category of Locally Preordered Spaces Sanjeevi Krishnan, 2009, Applied Categorical Structures vol. 17, 5, 445-466
^ Categories and Groupoids, Philip J. Higgins, Van Nostrand Reinhold, 1971
^ Topology and Groupoids. Ronald Brown. Booksurge LLC, 2006
^ Reparametrization of Continuous Paths. Ulrich Fahrenberg and Martin Raussen. Journal of Homotopy and Related Structures, vol. 2(2), 2007, pp.93–117
^ Components of the Fundamental Category. L. Fajstrup, E. Goubault, E. Haucourt, and M. Raussen. App. Cat. Struct. 12(1), 81-108, 2004
^ Generalized Congruences — Epimorphisms in $Cat$ Theory and Applications of Categories 5(11) 266–280, 1999
^ Categories of Components and Loop-Free Categories Emmanuel Haucourt, Theory and Applications of Categories 16(27), 736–770, 2006
^ Model Category. Mark Hovey, AMS, 1999